The term "square root" usually refers to the definition:

A number which when squared gives the desired result.

By convention, when we take the square root of a real number the result (if it exists) is positive (or non-negative).

Thus:

The square root of 9 is 3

by convention, not -3, even though $(-3)^2=9$

The square root of 0 is 0.

There is no square root of -4

restricting ourselves to the real numbers

We can take the square root of negative real numbers by using imaginary numbers.

When we take the square root of a complex number there is no concept of "positive" so the convention fails and we must then consider both square roots.

By restricting the square root of positive real numbers to the positive result, the square root operation is a function:

$\sqrt{}:\mathbb{R}^+\mapsto\mathbb{R}^+$

See also:
Domain of a function

Image of a function

The domain of the function is the non-negative real numbers, and (using our convention) the image is also the non-negative real numbers.

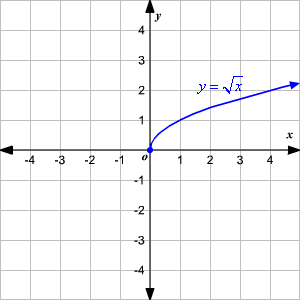
When taking the square root of a complex number we have more of a problem. The square root is now defined for every complex number, but every complex number (except 0) has two square roots. That means the square root operation is not a function. Trying to choose one of the square roots over the other doesn't solve the problem completely satisfactorily.

It's nice for functions to be continuous, with the result varying slowly as we vary the input. However, consider the square root of 9. Choose one of the roots, say 3. Now move the input point around in a circle of radius 9 anti-clockwise and the square root also moves in a circle anti-clockwise, but only half as fast. As the input point gets to -9 the square root is $3i.$ By the time the input point gets back to its starting point of 9, the output point, the square root, has only got as far as -3. Arbitrarily choosing just one of the square roots means the result cannot be continuous.

We can solve this by using a Riemann Surface, and more generally, operations that have more than one possible answer can be made one-to-one by using a Riemann surface as the CoDomain. (See CoDomain of a function)

See: http://en.wikipedia.org/wiki/Riemann_surface

ArgandDiagram BasinOfAttraction ComplexNumber ComplexPlane CubeRoot FundamentalTheoremOfAlgebra GerolamoCardano NewtonsMethod RootsOfPolynomials	Logarithm TypesOfNumber			A4Paper AGentleIntroductionToNPC CancellingFractions CommonFactor ContinuedFraction DedekindCut DomainOfAFunction EIsIrrational Euclid MathematicsTaxonomy ModuloArithmetic PiIsIrrational Pythagoras RationalNumber RationalisingTheDenominator RealNumber ScalarProduct TimeComplexity UnitVector
↓	↓		↓	↓
ImaginaryNumber RiemannSurface Root			AGentleIntroductionToTimeComplexity AbsoluteValue AlgebraicNumber EuclideanAlgorithm FactoringQuadratics InverseFunction IrrationalNumber MagnitudeOfAVector RootTwoIsIrrational Surd
			↓
		⇌	You are here SquareRoot
			↓
			CoDomainOfAFunction ComplexNumber DomainOfAFunction Function ImageOfAFunction RealNumber
↓	↓		↓	↓
BernhardRiemann CubeRoot FundamentalTheoremOfAlgebra HolomorphicFunction Logarithm NewtonsMethod RiemannHypothesis	ComplexPlane			AddingComplexNumbers AlgebraicNumber ArgandDiagram CategoryMetaTopic CauchySequence ComplexConjugate ContinuedFraction DedekindCut DividingComplexNumbers Euler Integer IrrationalNumber MultiplyingComplexNumbers PolarRepresentationOfAComplexNumber Polynomial RangeOfAFunction RationalNumber TranscendentalNumber

Local neighbourhood - D3

Last change to this page
Full Page history
Links to this page

Edit this page
(with sufficient authority)
Change password

Recent changes
All pages
Search

Square Root

Navigation

You are here

Local neighbourhood - D3